A reader writes: “How would you equate or gauge the Big Price to a 12 man 5X5 mixed league auction with $260. We play keepers too but that’s really not my issue. The Big Number seems to be about right as most other magazines I’ve seen will list auction prices using that format.”
I’ve answered this question before, and published an article showing how to do the math in 2014. Click here to read that.
But before you do that, you may want to read this.
The prices in The Guide are for a 24-team mixed league, and are intended to emulate the pricing of a deep AL and NL only leagues. The reason I don’t publish AL and NL only prices—the leagues are a little different, which makes the values of their stats a little different—is because when we put together the Guide in December there are usually hundreds of free agents out there. We don’t know who is going to be in which league.
The important thing to remember about deep prices is that the value of the stats, be they homers, RBIs, runs, hits, steals, are linear. That means that every home run a batter hits has the same value. Every stolen base has the same value. Et cetera. The reason for this is because the vast majority of stats that are produced in the whichever league one is playing in are counted in your roto standings. The replacement level is pretty close to nil for any stat category.
In a 12-team mixed league, you’re playing with just 12 of baseball’s 30 teams. You’re only using the half the available stats overall, roughly (this varies by category). This means that a player has to hit a bunch of homers before those homers have any value. And if he doesn’t hit them, there will someone available for free who will.
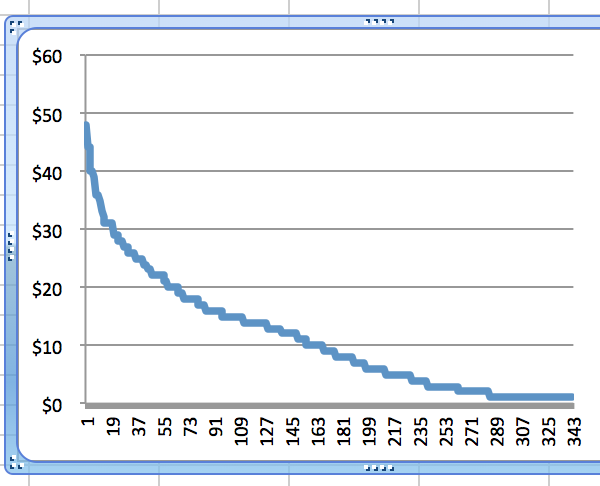
What this means, practically, is that in a AL or NL only league, the last player taken costs $1. And in a 12 team mixed league the last player taken cost $1. But the last player taken in the mixed league would have cost about $13 in the only league. The chart below shows the prices for players taken in a 15-team mixed auction, likely Tout Wars in 2016, from most expensive to least.
The thing to notice is that the graph goes pretty straight at about the 50th player taken, which supports the observation that after the third round in a mixed draft the players in each round are pretty interchangeable. No matter who someone takes, there’s another player like him still available. But this isn’t so among the best players. They are not interchangeable, and their value drops quickly, as the left side of the graph shows.
When someone takes Mike Trout, there isn’t another Mike Trout out there. There is Jose Altuve, but when he’s gone there isn’t someone similar. By the time you get to the sixth or seventh player the options are not nearly as appealing as the early choices were. In a draft, the compensation is the earlier pick in the next round. In an auction there is no compensation. Those irreplaceable players can only go to the person who pays for them, and that drives their prices up. Hence the steep curve in the graph showing the prices of the best players.
This situation is even more extreme in a 12-team league than a 15-team league. The bottom line is that if you convert the magazine prices to your mixed league size, it is important that you then reallocate money from the least expensive end of the list to the most expensive end, so that you have realistic prices for the Trouts, Turners, and Scherzers in your game.
Your draft day goal is to have a list that shows the prices you’re willing to pay for each available player, and have that add up to the amount of money available in your auction.
You don’t have to buy those most expensive players. In this year’s Guide, Tout Mixed Auction 2017 winner Jeff Zimmerman talks about how the prices for the top guys in that auction were overinflated. He complains that people always inflate the prices of the top guys in mixed auctions, as if that’s a mistake. I think Jeff is such a numbers guy that he only looks at what people earned to determine their price, and from his success you can see that his price list can work. But I think his list worked in spite of his error, rather than because of it.
What makes me think so? The graph above.